Shortest Path Examples
These examples are based on the Traversal Graph. Create a graph based on the example graph to follow along.
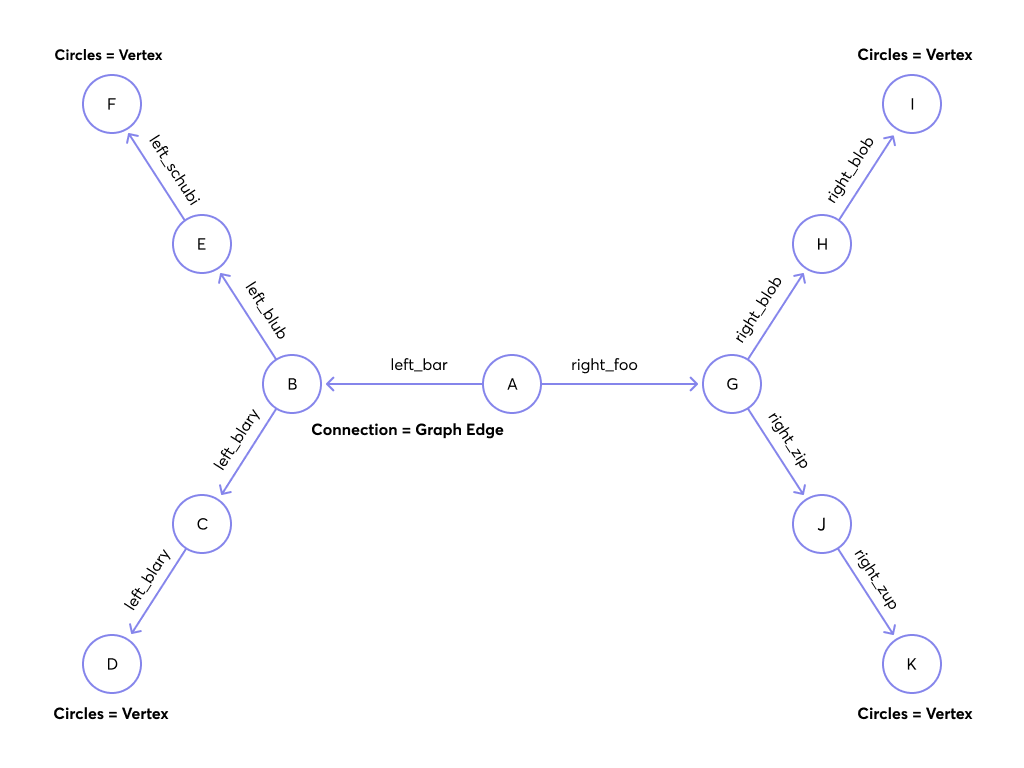
Shortest Path Example
You can query the shortest path from A to D using either the named graph syntax or the collection sets syntax. The results are identical. For information about running queries, refer to Running Queries.
Named Graph
FOR v, e IN OUTBOUND SHORTEST_PATH 'circles/A' TO 'circles/D' GRAPH 'traversalGraph'
RETURN [v._key, e._key]
This query uses the named graph 'traversalGraph' and the OUTBOUND keyword to traverse from the start vertex 'circles/A' to the target vertex 'circles/D'. The SHORTEST_PATH keyword ensures that only the shortest path is returned.
The RETURN statement returns an array containing the _key attributes of both the vertex (v._key) and the edge (e._key) of each step along the path. Because this query is using a named graph, the edge collections are inferred from the graph and do not need to be specified explicitly.
Collection Sets
FOR v, e IN OUTBOUND SHORTEST_PATH 'circles/A' TO 'circles/D' edges
RETURN [v._key, e._key]
This query specifies the edge collection to traverse (edges). The OUTBOUND keyword is used to traverse in the outbound direction from the start vertex 'circles/A' to the target vertex 'circles/D'. The SHORTEST_PATH keyword ensures that only the shortest path is returned.
The RETURN statement returns an array containing the _key attributes of both the vertex (v._key) and the edge (e._key) of each step along the path.
Traverse Mixed Directions Example
You can also compute shortest paths based on documents found in collections. You can use either the named graph syntax or the collection sets syntax, the results are identical. For information about running queries, refer to Running Queries.
Named Graph
LET a = (FOR a IN circles FILTER a._key == 'A' return a)[0]
LET d = (FOR d IN circles FILTER d._key == 'D' return d )[0]
FOR v, e IN
OUTBOUND SHORTEST_PATH a TO d
GRAPH 'traversalGraph'
RETURN [v._key, e._key]
This query uses a named graph. It first filters the vertex with the key 'A' from the 'circles' vertex collection and assigns it to variable 'a'. Similarly, it filters the vertex with the key 'D' from the 'circles' vertex collection and assigns it to variable 'd'. It then finds the shortest path between vertex 'a' and vertex 'd' using the 'traversalGraph' named graph.
The RETURN statement returns an array containing the _key attributes of both the vertex (v._key) and the edge (e._key) of each step along the path.
Collection Sets
LET a = (FOR a IN circles FILTER a._key == 'A' return a)[0]
LET d = (FOR d IN circles FILTER d._key == 'D' return d )[0]
FOR v, e IN
OUTBOUND SHORTEST_PATH a TO d edges
RETURN [v._key, e._key]
This query uses a collection set instead of a named graph. It first filters the vertex with the key 'A' from the 'circles' vertex collection and assigns it to variable 'a'. Similarly, it filters the vertex with the key 'D' from the 'circles' vertex collection and assigns it to variable 'd'. It then finds the shortest path between vertex 'a' and vertex 'd' using the edge collections specified in the 'edges' collection set.
The RETURN statement returns an array containing the _key attributes of both the vertex (v._key) and the edge (e._key) of each step along the path.
Results
Your results will be similar to the following. They will not be identical, because the edges of the Traversal Graph in the Example Graphs are created with randomly assigned _KEY values.
[
[
"A",
null
],
[
"B",
"4464905920"
],
[
"C",
"4464905922"
],
[
"D",
"4464905924"
]
]