Multiple Path Search (MPS) Example

The shortest path algorithm is designed to find a single shortest path between two vertices. However, in some cases, there might be multiple shortest paths with the same length, and you might want to retrieve all of them.

Consider the following graph:

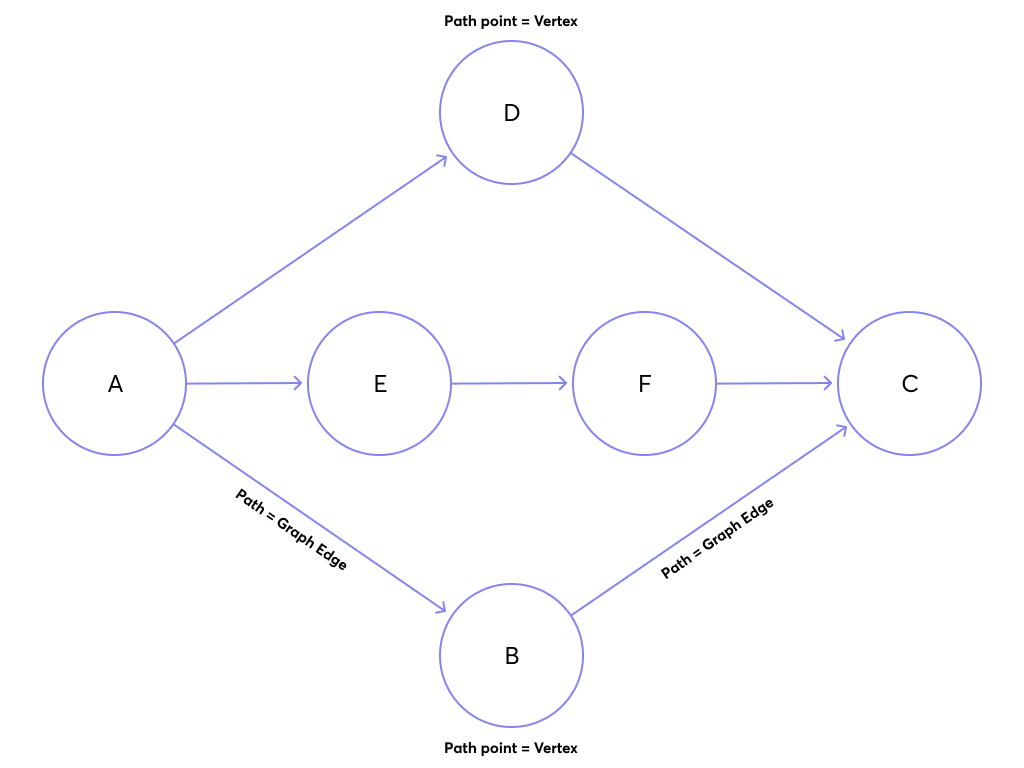
A shortest path query from A to C might return either A -> B -> C or A -> D -> C, but it's not guaranteed which one will be returned (ignoring edge weights in this example).

MPS Example Data

MPS vertices, import into Document collection called mps_verts:

[
  {
    "_key": "A"
  },
  {
    "_key": "B"
  },
  {
    "_key": "C"
  },
  {
    "_key": "D"
  },
  {
    "_key": "E"
  },
  {
    "_key": "F"
  }
]

MPS edges, import into Graph Edge collection called mps_edges:

[
  {
    "_from": "mps_verts/A",
    "_key": "-7Xtc1p2KF29QoN8LxJzNx-",
    "_to": "mps_verts/B",
    "vertex": "A"
  },
  {
    "_from": "mps_verts/A",
    "_key": "-Zc3OSyobGuukQ5S6HTLoGV",
    "_to": "mps_verts/E",
    "vertex": "A"
  },
  {
    "_from": "mps_verts/A",
    "_key": "-uAAL2GIhG5eAvGZruTF_2-",
    "_to": "mps_verts/D",
    "vertex": "A"
  },
  {
    "_from": "mps_verts/B",
    "_key": "-iRi0o8SmHJHaQ26axgFe3F",
    "_to": "mps_verts/C",
    "vertex": "B"
  },
  {
    "_from": "mps_verts/D",
    "_key": "-xaQUYPtzIuTbMm2Fynv3qV",
    "_to": "mps_verts/C",
    "vertex": "D"
  },
  {
    "_from": "mps_verts/E",
    "_key": "-fkKrokGqFP56aKHZbeMHJk",
    "_to": "mps_verts/F",
    "vertex": "E"
  },
  {
    "_from": "mps_verts/F",
    "_key": "-JOT3Np0FGd5zcs02dDNTmV",
    "_to": "mps_verts/C",
    "vertex": "F"
  }
]

Finding the Shortest Path Length

You can use the following query to determine the shortest path length:

RETURN LENGTH(
  FOR v IN OUTBOUND
    SHORTEST_PATH "mps_verts/A" TO "mps_verts/C" mps_edges
      RETURN v
)   

For the example graph, the result is 3, which includes the start vertex. Subtract 1 to get the edge count or traversal depth.

Retrieving All Paths with the Shortest Length

To find all paths with the determined length, use a pattern matching traversal. Start at vertex A and filter the results to only retrieve paths that end at vertex C.

The following query returns all paths with a length of 2, starting at vertex A and ending at vertex C:

FOR v, e, p IN 2..2 OUTBOUND "mps_verts/A" mps_edges
    FILTER v._id == "mps_verts/C"
      RETURN CONCAT_SEPARATOR(" -> ", p.vertices[*]._key)

Result:

[
    "A -> B -> C",
    "A -> D -> C"
]

A traversal depth of 3..3 would return A -> E -> F -> C and 2..3 would return all three paths.

Limitations

To achieve this result, two separate queries are required:

1. First, compute the shortest path length.
2. Then, based on the shortest path length (minus 1), perform the pattern matching.

This is because the min and max depth parameters in the traversal query cannot be expressions. They must be known in advance, either as number literals or bind parameters.